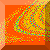
Pattern Formation
Chaotic Advection of Passive Scalar
The distribution of dye in a fluid undergoing chaotic motion
evolves in such a way that the gradient of the dye
density increases with time and the region where the
dye density gradient is largest becomes more and more
striated into thinner and thinner ribbon-like regions,
eventually concentrating on a fractal set. These
pictures show the early stage of this process.
(175K) 
(108K)
(105K)
Reference: F. Varosi, T.M. Antonsen and E. Ott,
"The spectrum of fractal dimensions of passive scalar
gradients in chaotic fluid flows",
Phys. Fluids A, vol. 3, p.1017 (1991)
Two Dimensional Turbulence
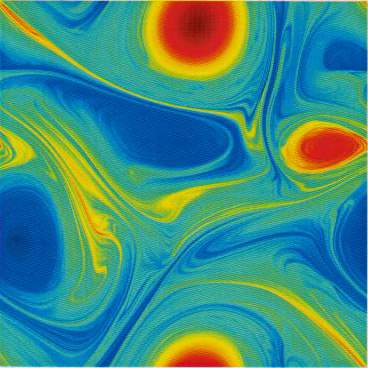
Description: This picture shows the vorticity field in two
dimensional turbulence with a drag force proportional to velocity
added to the right hand side of the Navier-Stokes momentum equation.
We find that the energy wavenumber spectum in the presence of drag
scales like k-(3+n), n > 0, in contrast to the
classical k-3 behavior without drag.
[K. Nam, et al., Phys. Rev. Lett., 84, 5134(2000)]
(PDF)
Description: This picture shows the blow-out solutions in two
dimensional turbulence of Ginzburg-Landau Equation with a parameteric
force. We find that the probability density function of the amplitude
has a exponential tails.
Description:
The phase field resulting from a simulation of the complex Ginzburg-Landau equation.
Several frames from a 100 x 100 domain with 512x512 grid points. See
Target waves in the complex Ginzburg-Landau equation, Phys. Rev. E 62, 7627-7631 (2000)
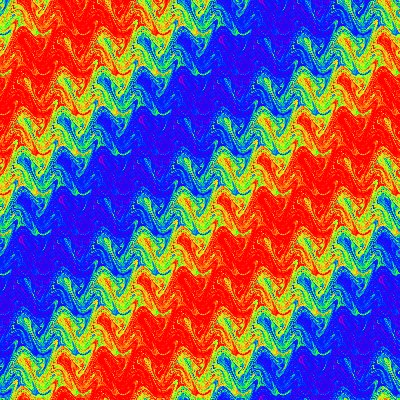
Description: A false color image of scalar that is passively
advected by a chaotic fluid flow. The underlying flow has a spatial
period that is one tenth that of the scalar. This gives rise to the
small scale structure that is nearly periodic and modulated at the
largest scale.
(175K) 
(108K)
(105K)
