 Research Interests Research Interests
In the beginning, how the heav'ns and earth rose out of chaos
- John Milton.
In this section we briefly explained many of our theoretical research interests
and, if possible, we provide some references in the general science
literature. For works of a more technical nature please refer to the
papers section or click the appropriate
paper icon below for the topic of your choice. For a brief overview of chaos
we refer you to
- C. Grebogi, E. Ott, and J.A. Yorke, "Chaos, Strange Attractors, and Fractal Basin Boundaries in Nonlinear Dynamical Systems", Science, 238, 585 (1987).
For a more extensive treatment see the book
The following list should come in handy for navigational
purposes:
In the classical dynamics potential scattering problem one considers a
Hamiltonian H = p /2m + V(r), where the potential V approaches
zero for large r (the magnitude of r) . One then asks how
outgoing orbits at large r depend on incoming orbits. For example, one
might plot scattering angle as a function of impact parameter. In
typical cases, such functions can have exceedingly complex behavior,
where the function is singular on a fractal (uncountable) set of
impact parameter values. This type of behavior is indicative of the
presence of an unstable chaotic set in the dynamics. /2m + V(r), where the potential V approaches
zero for large r (the magnitude of r) . One then asks how
outgoing orbits at large r depend on incoming orbits. For example, one
might plot scattering angle as a function of impact parameter. In
typical cases, such functions can have exceedingly complex behavior,
where the function is singular on a fractal (uncountable) set of
impact parameter values. This type of behavior is indicative of the
presence of an unstable chaotic set in the dynamics.
- Maddox, John, "Is Chaos becoming conversational?", Nature,
341, No. 7, pg. 17, Sept. 1989.
Chaotic Transients
In chaotic transients one observes that typical initial conditions
initially behave in an apparently chaotic manner for a possibly long
time, but, after a while, then rapidly move off to some other region
of phase space, perhaps asymptotically approaching a nonchaotic
attractor. The length of such chaotic transients depends sensitively
on initial conditions and exhibits a characteristic Poisson
distribution for randomly chosen initial conditions.
Communicating with Chaos
Much of the fundamental understanding of chaotic dynamics involves
concepts from information theory, a field developed primarily in the
context of practical communication. Concepts from information theory
used in the chaos includes metric entropy, topologoical entropy,
Markov partitions, and symbolic dynamics. It is possible to use the
close connection between the theory of chaotic systems and information
theory in a way that is more than purely formal. In particular, it can
be shown that the recent realization of chaos can be controlled with
small perturbations can be utilized to cause the symbolic
dynamics of a chaotic system to track a prescribed symbol sequence
thus allowing the encoding of any desired message in the
signal from a chaotic oscillator. The natural complexity of chaos thus
provides a vehicle for information transmission in the usual sense.
Two fundamental aspects of chaos are the following:
- The exponential sensitivity of orbits to small perturbations.
- A very complex orbit structure making possible many very different
motions in the same system.
Actually these two are not independent; they may be viewed as two sides
of the same "chaos coin". The first property leads to the diffculty in the
prediction of sufficiently distant future states, while the second property
leads to the fact that chaotic attractors often have embedded within them
an infinite, dense set of unstable periodic orbits. While chaos is commonly
viewed as undesirable, these properties can also be of great benefit in
certain situations where one wishes to control the system dynamics. In
particular, if the system is sufficiently well characterized and noise is
not too large, then the first property implies that relatively large changes
in the eventual location of orbit points can be made using only small changes
in a control variable, while the second property implies that the dynamical
changes so produced may be very diverse, leading to a situation with a
great deal of flexibility. The two methods that are useful in utilizing chaos
in an effective ways are:
 Control Control-
Feedback stabilization of selected unstable orbits embedded in the attractor.
 Targeting Targeting-
The rapid steering of a chaotic orbit to the vicinity of a desired point in phase space.
- T. Shinbrot, C. Grebogi, E. Ott, and J.A. Yorke, "Using Small Perturbations to Control Chaos", Nature, 363, 411 (1993).
- Peterson, Ivars, "Ribbon of Chaos" Science News, 139, No. 4, pg. 60,
Jan. 26, 1991.
- Langreth, Robert, "Engineering Dogma gives way to Chaos",
Science, 252, pg. 776, May 1991.
- Corcoran, Elizabeth, "Ordering Chaos", Scientific American,
pg. 96, Aug. 1991.
Another type of transition to a chaotic attractor is the crises. Basically, what
happens in this case is that the unstable chaotic set responsible for a chaotic transient becomes stable as the parameter
p is increased through a critical crisis value p . When it becomes stable, the chaotic set formerly responsible for the chaotic transient becomes a chaotic
attractor. For parameter values in the transient range, p > p . When it becomes stable, the chaotic set formerly responsible for the chaotic transient becomes a chaotic
attractor. For parameter values in the transient range, p > p , there is typically a characteristic dependence of the mean duration of chaotic transients on
p. Namely, , there is typically a characteristic dependence of the mean duration of chaotic transients on
p. Namely,
 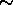 (p-p
(p-p ) )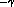 , where the critical exponent , where the critical exponent 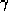 can be obtained from a
knowledge of the instability properties of certain unstable periodic
orbits on the chaotic set. This dependence of can be obtained from a
knowledge of the instability properties of certain unstable periodic
orbits on the chaotic set. This dependence of  on
p makes clear the
nature of the transition: on
p makes clear the
nature of the transition:  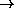  as
p as
p  p p from below, thus converting the transient to long-term time-asymptotic
behavior.
from below, thus converting the transient to long-term time-asymptotic
behavior.
Perhaps the most basic aspect of an attractor is its dimension. While it is clear
that the dimension of a fixed point in phase space is zero and that of the
limit cycle is one, it is also the case that invariant sets arising in dynamical
systems (such as chaotic attractors) often have structure on arbitrarily fine
scale, and the determination of the dimension of such sets is nontrivial. In such
cases the assignment of a dimension value gives a much needed quantitative
characterization of the geometrical structure of a complicated object.
Magnetic fields are pervasive in the Universe. A natural
approach to explain their prevalence is the kinematic dynamo problem: Given a flow of a conducting fluid, will a small
seed magnetic field amplify exponentially with time? If the answer is yes then the zero magnetic field state is
unnatural, and the flow will self-generate its own magnetic field. Recently it has been shown that chaos in the Lagrangian
dynamics of the underlying flow is the key consideration for answering the question posed by the kinematic dynamo problem.
Basin boundaries arise in dissipative dynamical systems when two, or
more, attractors are present. In such situations each attractor has a
basin of initial conditions which lead asymptotically to that
attractor. The basin boundaries are the sets which separate different
basins. It is very common for basin boundaries to contain unstable
chaotic sets. In such cases the basin boundaries can have very
complicated fractal structure. Because of this complicated very
fine-scaled structure, fractal basin boundaries can pose an impediment
to predicting long-term behavior. In particular, if an initial
condition is specified with only finite precision, it may be very
difficult a priori to determine in which basin it lies if the
boundaries are fractal.
The interconnection of large numbers of dynamical units is common across a variety
of fields including such applications as the internet, the world wide web, gene networks,
and the web of social interactions between people, corporations, and animals.
Recent research in this area has focused on characterizing network properties, on the
evolution and growth of networks, and on the relation of network topology to the
dynamics and functioning of networked systems.
Pattern formation in non-equilibrium systems has drawn intensive
attention and
has been the subject of much rigorous investigation in recent years.
Belousov-Zhabontinskii(BZ) chemical reaction, colonies of social
amoebaem, electical excitation propagation in the heart are situations where considerations of spatiotemporal pattern
dynamics are important.
As the simplest description of such systems, we have investigated various aspects of the Complex Ginzburg
Landau Equation, especially the formation of spiral waves.
Prediction
One of the fundamental characteristics of chaotic processes is the
failure of long-term predictability. Unlike nonchaotic cases, where
the system settles into an equilibrium or regular oscillatory mode, a
system whose evolution is described by a chaotic attractor exhibits
many of the properties of a random process. In fact, this superficial
resemblance of a chaotic process to a random process was one of the
reasons that chaos was not generally recognized in practice until
recent years. Systems that entered a regime in which they oscillated
irregularly were equated with random processes, and therefore
considered unpredictable except in a statistical way. More recently methods of short-term prediction of chaotic processes
have been formulated. These methods make use of the ergodicity of orbits on chaotic attractors. In particular, ergodicity
implies the ability to learn dynamics from observations of the system and then use that knowledge for prediction.
According to the correspondence principle, there is a limit where
classical behavior as described by Hamilton's equations becomes
similar, in some suitable sense, to quantum behavior as described by
the appropriate wave equation. Formally, one can take this limit to be
h approaching zero, where h is Planck's constant; alternatively, one
can look at successively higher energy levels, etc. Such limits are
referred to as "semiclassical". It has been found that the
semiclassical limit can be highly nontrivial when the classical
problem is chaotic. The study of how quantum systems, whose classical
counterparts are chaotic, behave in the semiclassical limit has been
called quantum chaos. More generally, these considerations also apply
to elliptic partial differential equations that are physically
unrelated to quantum considerations. For example, the same questions
arise in relating classical acoustic waves to their corresponding ray
equations. Among recent results in quantum chaos is a prediction
relating the chaos in the classical problem to the statistics of
energy-level spacings in the semiclassical quantum regime.
The notion of determinism in classical dynamics has eroded since
Poincaré's work led to recognition that dynamical systems can exhibit
chaos: small perturbations grow exponentially fast. Hence,
physically ubiquitous measurement errors, noise, and computer
roundoff strongly limit the time over which, given an initial
condition, one can predict the detailed state of a chaotic
system. Practically speaking, such systems are nondeterministic.
Notwithstanding the quantitative uncertainty caused by perturbations, the
system state is confined in phase space (on an "attractor") so at least
its qualitative behavior is predictable. Another challenge to
determinism arises when systems have competing attractors. With a
boundary (possibly geometrically convoluted ) between sets of
initial conditions tending to distinct attractors ("basins of
attraction"), perturbations make it difficult to determine the fate
of initial conditions near the boundary. Recently, mathematical
mappings were found that are still worse: an attractor's entire basin
is riddled with holes on arbitrarily fine scales. Here,
perturbations globally render even qualitative outcomes
uncertain; experiments lose reproducibility.
- J.C. Sommerer and E. Ott, "A Qualitatively Nondeterministic Physical System", Nature, 365, 135 (1993).
Chaotic processes have the property that relatively small numerical
errors tend to grow exponentially fast. In an iterated process, if
errors double each iterate and numerical calculations have 48-bit (or
15-digit) accuracy, a true orbit through a point can be expected to
have no correlation with a numerical orbit after 50 iterates. One may
therefore question the validity of a computer study over times longer than this relatively short time. A relevant result in
this regard is that of Anosov and Bowen who showed that systems which
are uniformly hyperbolic will have the shadowing property: a numerical
(or noisy) orbit will stay close to (shadow) a true orbit for all
time. Unfortunately, chaotic processes typically studied do not have
the requisite uniform hyperbolicity, and the Anosov-Bowen result does
not apply. Recent results of our group apply to nonhyperbolic situations.
- Cipra, Barry A., "Computer-Drawn Pictures Stalk the Wild Trajectory",
Science, 241 pg. 1162, Sept. 1988.
- Peterson, Ivars, "In the Shadow of Chaos", Science News, 134, No. 23,
pg. 360, Dec. 3, 1988.
- Maddox, John, "How to shadow noisy chaos", Nature, 347, No. 18,
pg. 613, Oct. 1989.
Unstable Chaotic Sets
Attractors refer to sets which "attract" orbits and hence determine
typical long-term behavior. It is also possible to have sets in phase
space on which the dynamics can be exceedingly complicated, but which
are not attracting. In such cases orbits placed exactly on the set
stay there forever, but typical neighboring orbits eventually leave the
neighborhood of the set, never to return. One indication of the
possibility of complex behavior on such nonattracting (unstable) sets
is the presence within these sets of periodic orbits whose number increases exponentially with their
period, as well as the presence of an uncountable number of
nonperiodic orbits. Nonattracting unstable chaotic sets can
have important observable macroscopic consequences. Three such
consequences are the phenomena of chaotic transients, fractal basin
boundaries, and chaotic scattering.
|

