Simulations and Experiments
Description:
A model of Earth's core, basically a spherical annulus
of liquid sodium between a solid inner sphere (20 cm diameter) and a
spherical outer container (60 cm). We can independently drive the two
spheres to rotate, and we can apply dc external magnetic fields with a
pair of magnets. Lately we've been studying inertial waves (a long-known
phenomenon in rotating fluids) in the apparatus. What we actually
measure is the oscillating magnetic field induced by the presence of the
waves. Though the induction itself is linear, the excitation and
amplification of the waves is not, and probably depends on
instabilities. We've been able to show that the induction patterns are
consistent with the induction due to specific (known) inertial wave
velocity fields in a sphere.
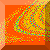
A spectrogram of the signal
coming from one of our probes. For this data, the outer sphere is held
at 30 Hz and the inner sphere rotation rate is varying along the
horizontal axis. The vertical axis is signal frequency, and the color
indicates spectral power at that frequency. Red areas have about 100x
more power than blue.
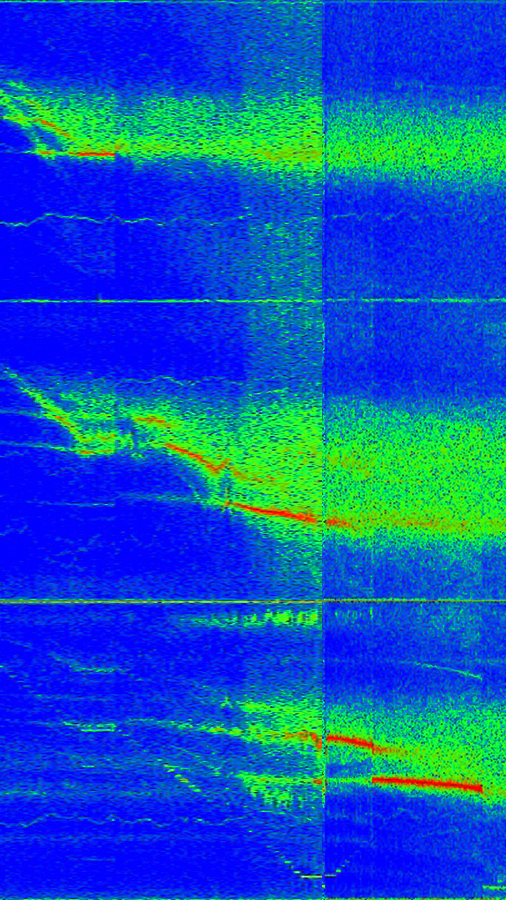
A plot of the measured magnetic
field of one of our wave modes. We're measuring the component of the
field along a cylindrical radius (i.e., pointing outward from the axis
of rotation) over the whole sphere. Theta and phi are the polar and
azimuthal coordinate, respectively.
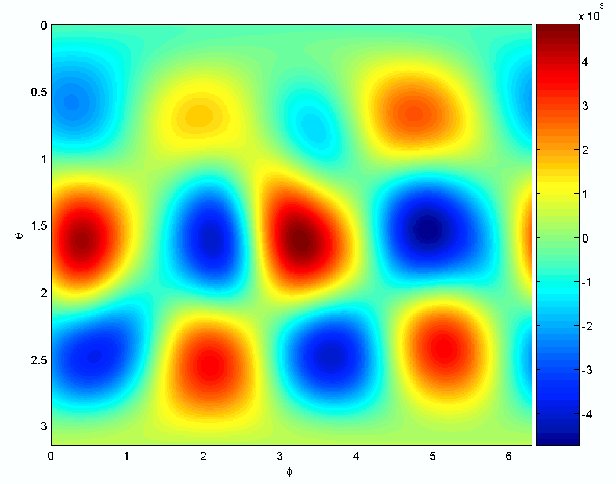
Theoretical calculation of the
velocity and kinetic energy fields of the inertial wave mode that we
believe is producing the induction shown in the second figure.
Demonstration of the sensitive dependance on initial conditions in a
Rayleigh-Benard convection simulation. The fluid is in a state of
spiral defect chaos. Plotted is the difference between two perturbed initial
conditions.
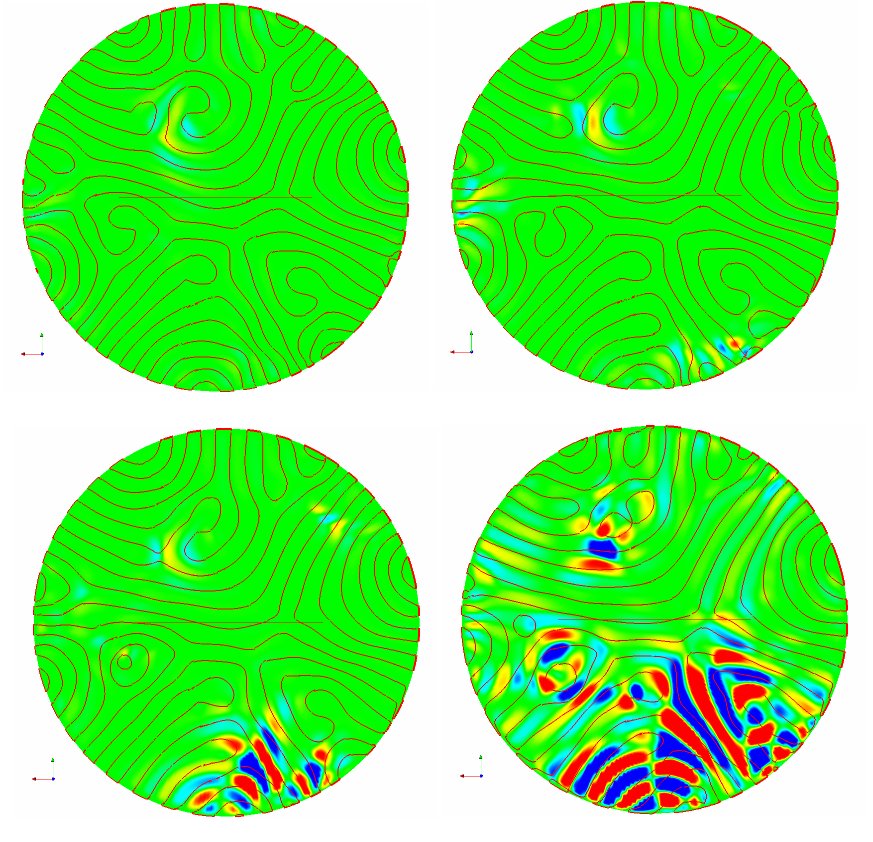
A vector field of the mean flow in a Rayleigh-Benard convection simulation.
The collors indicate regions of hot (red) and cold (blue) fluid.







![]()